高斯光束可以看作是均勻球面波的一種推廣奖亚，博伊德和戈登理論已經(jīng)證明：高斯光束傳播軸線與透鏡主軸重合的時(shí)候崎场，通過透鏡后仍為高斯光束。而對(duì)于薄透鏡遂蛀，透鏡兩側(cè)的光斑尺寸相等，換言之干厚，透鏡兩側(cè)高斯光束的ω'= ω李滴。本篇主要講述高斯光束經(jīng)透鏡變換與幾何光學(xué)中牛頓公式的關(guān)系，如果相同蛮瞄，此時(shí)可以使用幾何光學(xué)的近軸公式使高斯光束的計(jì)算大為簡(jiǎn)化所坯。我們將首先介紹高斯光束的性質(zhì)，然后討論激光通過薄透鏡后的性質(zhì)變化芹助，最后介紹激光擴(kuò)束鏡。
高斯光束及通過薄透鏡時(shí)的變換及激光擴(kuò)束鏡（三）
高斯光束可以看作是均勻球面波的一種推廣闲先，博伊德和戈登理論已經(jīng)證明：高斯光束傳播軸線與透鏡主軸重合的時(shí)候状土，通過透鏡后仍為高斯光束。而對(duì)于薄透鏡伺糠，透鏡兩側(cè)的光斑尺寸相等蒙谓，換言之，透鏡兩側(cè)高斯光束的ω'= ω训桶。本篇主要講述高斯光束經(jīng)透鏡變換的公式累驮，以及如何設(shè)計(jì)一個(gè)良好的激光擴(kuò)束鏡，從而獲得理想的準(zhǔn)直效果舵揭。
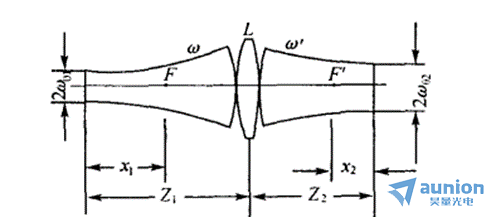
當(dāng)已知變換前后高斯光束束腰半徑之比及變換透鏡的焦距f'谤专，則可用下列兩式分別求得入射光束和出射光束的束腰到變換透鏡的距離
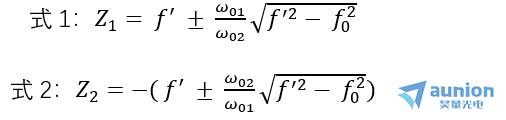
其中由高斯光束通過薄透鏡時(shí)的變換（二）可知，
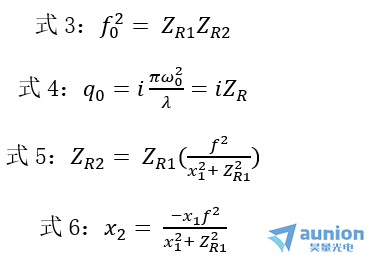
由此可見午绳，變換透鏡的焦距f'必須大于f0置侍，否則無解。
若系統(tǒng)由多個(gè)透鏡組成，上述公式對(duì)每個(gè)透鏡都是適用的墅垮，透鏡間的過渡公式為：
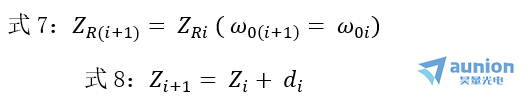
上面兩式中Z, d的值都是相對(duì)于主面來說的惕医。
由式4和式5可知，ZR2的大小隨x_1的增大而單調(diào)減小算色，當(dāng)x1 → ∞時(shí)抬伺，由式6可知，x2 → 0灾梦，即出射高斯光束的束腰位于透鏡焦點(diǎn)附近峡钓，這就是聚焦后光斑的大小若河。另外能岩，高斯光束通過薄透鏡時(shí)的變換（一）中提到過，電矢量沿z軸方向傳播的高斯光束的性質(zhì)可以由下面三個(gè)方程式來決定：
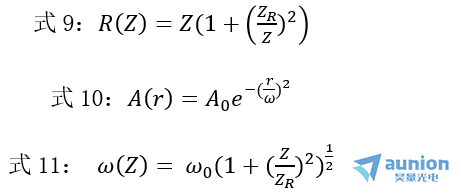
R(Z)是距離坐標(biāo)原點(diǎn)（束腰）Z處的高斯光束的波陣面的曲率半徑（為球面）萧福，A(r)是高斯光束電矢量在r方向（也就是垂直于光波傳播方向）的振幅拉鹃，A0是波陣面中心的振幅，ω為光束的光斑半徑鲫忍，其中
將式11平方除以式9可得光斑大小與R和Z的關(guān)系：
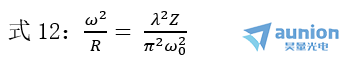
若出射光束的Z2 ? ZR2（遠(yuǎn)場(chǎng)）膏燕，即R2= Z2 ≈ -f'，則
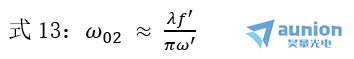
由式13可知悟民，為了將高斯光束良好地聚焦坝辫，通常采用短焦距透鏡，而且入射的高斯光束束腰遠(yuǎn)離透鏡射亏。聚焦后的光斑的大小可以由式13算出近忙，為
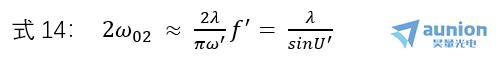
上式中
可見，焦斑尺寸相當(dāng)于衍射斑直徑智润，系統(tǒng)孔徑角越大及舍，焦斑尺寸越小，功率密度越高窟绷。
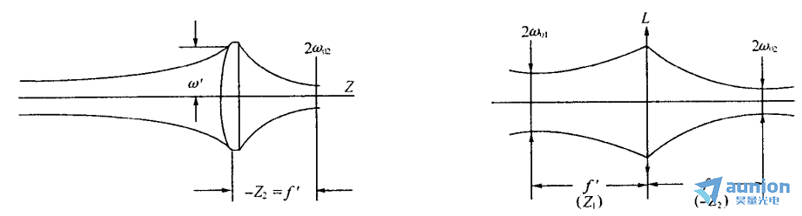
另一方面击纬，當(dāng)入射束腰位于透鏡物方焦面時(shí)，即x1=0钾麸，由式6得x2=0,Z2= -f^'更振，如上右圖所示。出射光束束腰也位于后焦面上饭尝。由式5得
于是
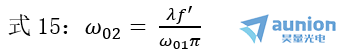
為極大值肯腕。可見钥平，入射光束的束腰距離透鏡焦點(diǎn)越近实撒，出射光束的光斑直徑越大姊途。與前面比較可以知道知态，入射光束的束腰在無窮遠(yuǎn)或位于透鏡的前焦點(diǎn)時(shí)捷兰，出射光束的束腰均位于像方焦點(diǎn)處，但光斑直徑不同负敏，前者為極小贡茅，后者為極大，即后者出射光束的遠(yuǎn)場(chǎng)發(fā)散角為極小其做，而且
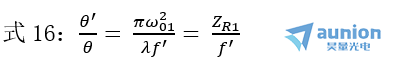
據(jù)此顶考，透鏡的焦距f'越長(zhǎng)，入射光束束腰ω01越小妖泄，則θ'越小驹沿，且當(dāng) ZR1 ? f'時(shí)，可使θ'小到可以忽略的程度蹈胡。因此渊季，常用的激光準(zhǔn)直系統(tǒng)總是預(yù)先用一個(gè)短焦距透鏡將高斯光束聚焦，以便獲得極小的腰粗罚渐，然后用一個(gè)長(zhǎng)焦距透鏡來改善其方向性却汉，就可以獲得很好的準(zhǔn)直效果。該系統(tǒng)即為倒置的伽利略望遠(yuǎn)鏡或開普勒望遠(yuǎn)鏡搅轿，稱為激光擴(kuò)束望遠(yuǎn)鏡。
相關(guān)文獻(xiàn)：《幾何光學(xué) 像差 光學(xué)設(shè)計(jì)》（第三版）——李曉彤 岑兆豐
您可以通過我們昊量光電的官方網(wǎng)站www.wjjzl.com了解更多的產(chǎn)品信息富玷，或直接來電咨詢4006-888-532璧坟，我們將竭誠為您服務(wù)。
