一篇帶你了解Allan 方差的數(shù)學(xué)基礎(chǔ)吉挣、用途概述以及如何使用Moku 相位表進(jìn)行相應(yīng)測量派撕。
Allan 方差理論及測量方法
Allan方差起初是為了評(píng)估原子鐘振蕩器的穩(wěn)定性而提出的，它提供了在不同時(shí)間尺度上頻率穩(wěn)定性的可靠測量睬魂，而標(biāo)準(zhǔn)偏差等統(tǒng)計(jì)量卻沒有考慮到這一點(diǎn)终吼。 在本白皮書中，我們將回顧 Allan 方差的數(shù)學(xué)基礎(chǔ)氯哮，并分享Allan 方差及其相關(guān)參量如何在振蕩器表征等實(shí)際應(yīng)用中成為精確分析時(shí)間序列數(shù)據(jù)的有用工具际跪。
利用Moku 我們可以執(zhí)行Allan 方差測量，Moku 是一種基于 FPGA 的設(shè)備喉钢，它包含了一整套可重構(gòu)的測試測量儀器姆打。相位表 是Moku上開發(fā)的高精度數(shù)字相位測量儀，我們可以超精確地記錄輸入周期信號(hào)的相位肠虽、頻率和振幅數(shù)據(jù)幔戏，也可以實(shí)時(shí)地計(jì)算和繪制 Allan 方差統(tǒng)計(jì)數(shù)據(jù)。
Allan 方差由來
您的系統(tǒng)穩(wěn)定性如何税课？有許多工具可以用來解答這個(gè)問題闲延。1960年 David W. Allan 在在美國guo家標(biāo)準(zhǔn)技術(shù)研究院（當(dāng)時(shí)稱為guo家標(biāo)準(zhǔn)局）研究光學(xué)時(shí)鐘時(shí)發(fā)明了一種全新的工具 [1]。
Allan 發(fā)現(xiàn)韩玩，隨著樣本數(shù)量增加垒玲，現(xiàn)有的統(tǒng)計(jì)指標(biāo)（例如標(biāo)準(zhǔn)差）對(duì)于特定噪聲源會(huì)出現(xiàn)偏差。 這促使他開發(fā)了一種新的時(shí)域計(jì)量方法找颓，今天該方法以他的名字命名合愈。
由于 Allan 當(dāng)時(shí)研究光學(xué)時(shí)鐘，所以為原子頻率鐘標(biāo)準(zhǔn)開發(fā)了 Allan 方差。因此想暗，該主題的討論經(jīng)常僅限于該領(lǐng)域的術(shù)語妇汗，特別是在表征振蕩器的頻率穩(wěn)定性方面帘不。
但是说莫，Allan方差可以針對(duì)任何時(shí)間序列進(jìn)行計(jì)算。 該序列可以代表信號(hào)自身寞焙，像溫度傳感器的輸出信號(hào)储狭，或其任意屬性（如頻率、相位捣郊、幅度等）辽狈，并以恒定的速率進(jìn)行評(píng)估。 因此呛牲，Allan 方差從通信 [2] 到導(dǎo)航 [3] 的各種應(yīng)用中備受青睞刮萌。
Moku 相位表提供了 Allan 方差作為一個(gè)數(shù)據(jù)后續(xù)處理的選項(xiàng)，如下方圖 1 Moku:Pro 相位表所示娘扩。本說明針對(duì)首次接觸的用戶提供了有關(guān)該統(tǒng)計(jì)方法的入門介紹着茸。
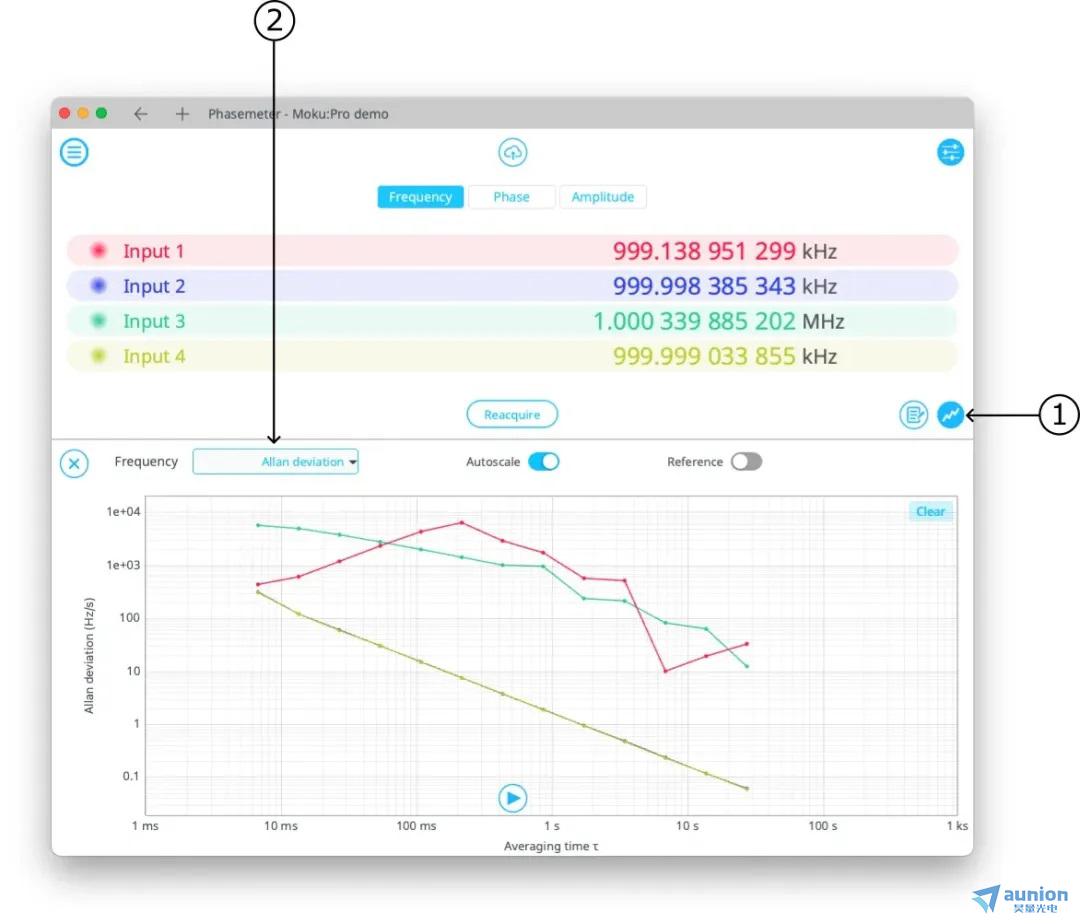
圖 1: 在相位表上顯示 Allan 標(biāo)準(zhǔn)差（Allan 方差的平方根），首先單擊數(shù)據(jù)圖形顯示按鈕琐旁。然后從下拉菜單選擇“Allan 標(biāo)準(zhǔn)差”涮阔。
Allan 方差數(shù)學(xué)運(yùn)算
Allan 方差的基本原理是將時(shí)間序列劃分為等分的部分，并考慮每等分的時(shí)間平均值與前一等分的時(shí)間平均值有何不同灰殴。 如果從整個(gè)數(shù)據(jù)集來看這些差異很小敬特，那么系統(tǒng)在這個(gè)時(shí)間尺度上是穩(wěn)定的。
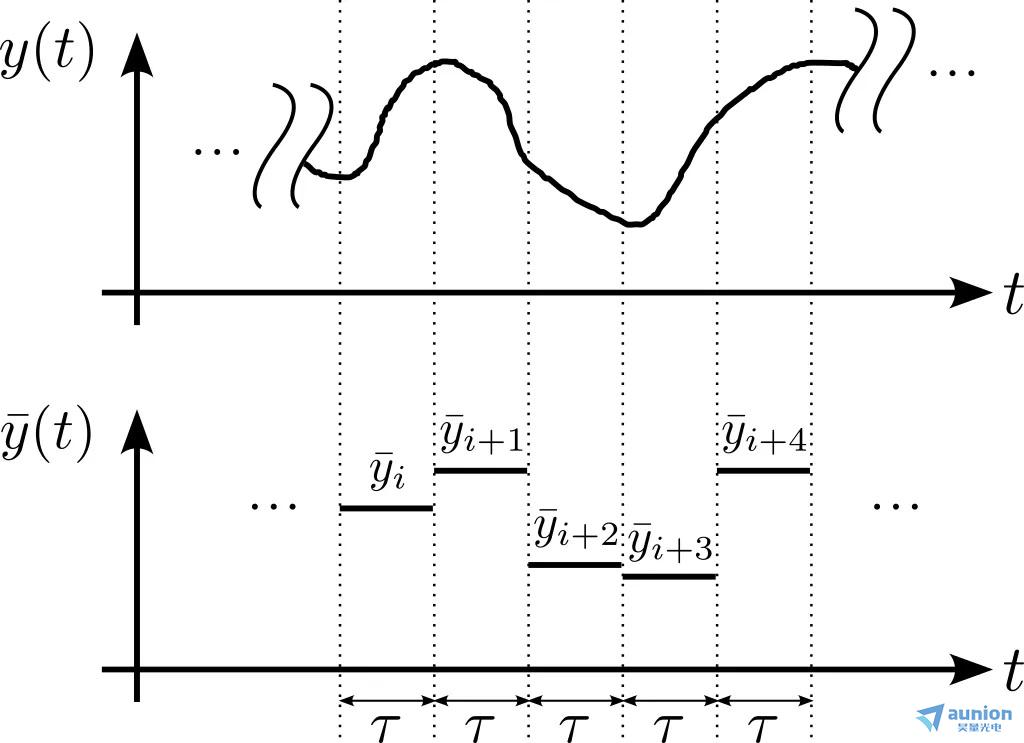
圖 2: 計(jì)算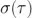 
第1步是將數(shù)據(jù)分割成長度為 τ 的片段并計(jì)算每一個(gè)分段 的時(shí)間平均值牺陶，伟阔。然后，我們減去連續(xù)平均值并計(jì)算這些差異的 RMS 值掰伸。將計(jì)算結(jié)果除以 得到觀測時(shí)間 τ 上的 Allan 方差皱炉。
更具體地說，假定我們有一個(gè)連續(xù)的時(shí)間序列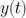 
碱工，其 Allan 方差 
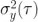定義為：
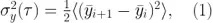
這里 <.> 表示期望值<平均值>娃承，同時(shí) 是 y 在觀測時(shí)間 τ 上的第 i 個(gè)樣本的平均值（圖 2）。Allan 標(biāo)準(zhǔn)差就是Allan 方差的平方根怕篷，或者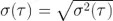 
历筝。我們可以針對(duì)一系列觀測時(shí)間 τ 評(píng)估該表達(dá)式，以深入了解數(shù)據(jù)在不同時(shí)間尺度上的自相似性（即穩(wěn)定性）廊谓。
從式（1）可以看出梳猪，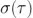
的維度與 y 相等。 我們將該值解釋為間隔 τ 秒的 y 測量值在兩個(gè) τ 秒之間的預(yù)期均方根差。
例如春弥，假定一個(gè)時(shí)鐘振蕩頻率在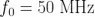 
呛哟。如果其分?jǐn)?shù)頻率差的 Allan 方差 - Y，表達(dá)式為：
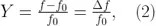
在10秒觀測時(shí)間 （τ = 10 s）上為 1.23x10-10 匿沛，然后我們可以預(yù)計(jì) Y 其兩個(gè)隨機(jī)選擇并連續(xù)的 10 秒觀測時(shí)間測量值相差為 1.23x10-10 RMS扫责。在給定的部分頻率差定義下，這等于一個(gè)預(yù)期的絕對(duì)頻率差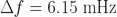 
逃呼。
現(xiàn)在我們思考長度為 M 的真實(shí)有限數(shù)據(jù)集的情況鳖孤，以周期 進(jìn)行采樣（圖 3）。我們不能在一個(gè)采集系統(tǒng)內(nèi)自由地選擇總時(shí)間 τ抡笼，所以我們將時(shí)長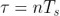 
劃分成 K 個(gè)數(shù)據(jù)分段苏揣，這里 
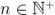。Allan 方差可以粗略地近似為：
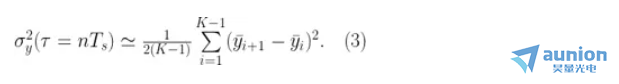
這里在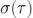 
的不確定度是 
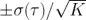推姻。測量不確定度的完整處理方法不在本文討論范圍之內(nèi)平匈，因此請(qǐng)參閱參考文獻(xiàn) [4] 了解更多詳細(xì)信息。為了改善結(jié)果的可靠性并且比較高效地使用數(shù)據(jù)值藏古，我們可以將數(shù)據(jù)劃分為重疊段（圖 4）增炭，這得到了 M-2n+1 對(duì)連續(xù)的分段，與之前的 K-1=M/n-1 正相反校翔。這樣重疊的 Allan 方差可以表示為：
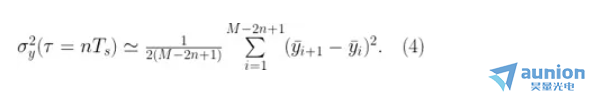
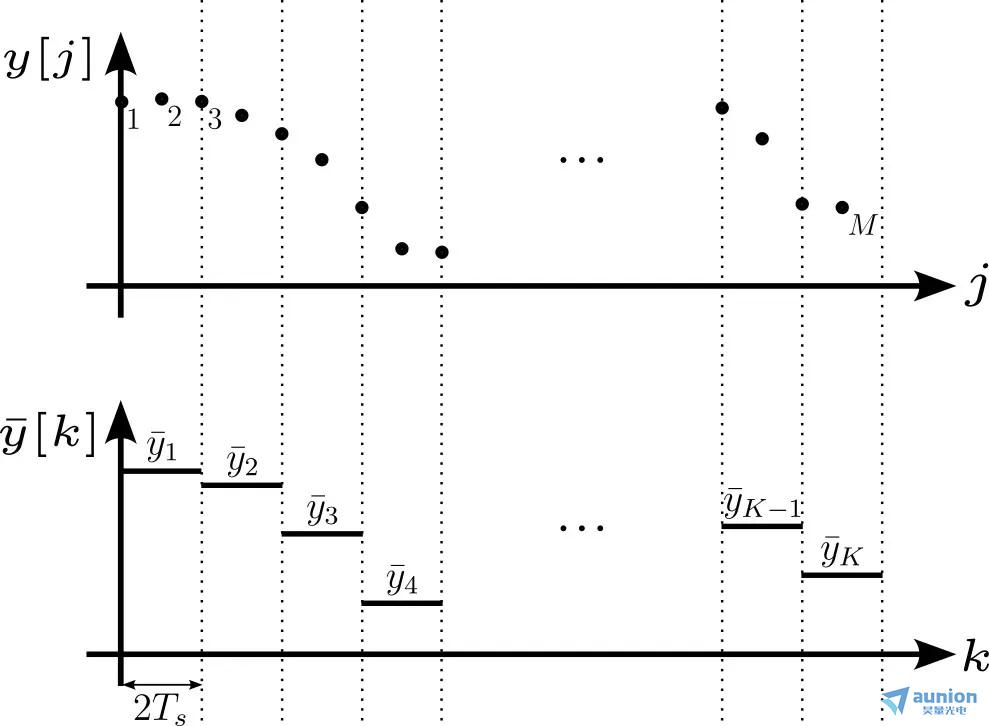
圖 3：在真實(shí)的采樣系統(tǒng)里弟跑，數(shù)據(jù)量是有限的，同時(shí) τ 被限制在幾倍采樣周期內(nèi)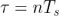 
（這里 n = 2）
通過積分獲得 Allan 方差
在許多常見的測量場景下存在一個(gè)變量 x防症，其屬性如下式所示：
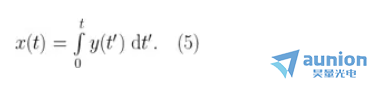
例如在時(shí)鐘穩(wěn)定度測量中孟辑，時(shí)間偏差 X 是部分頻率差 Y 的積分，例如在陀螺儀系統(tǒng)中蔫敲，被測角度饲嗽， θ 即旋轉(zhuǎn)速度 Ω 的積分。
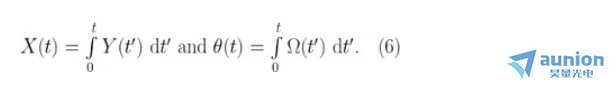
我們可以通過式（5）的積分來計(jì)算 x奈嘿，即使它不和某個(gè)被測物理量相對(duì)應(yīng)貌虾。
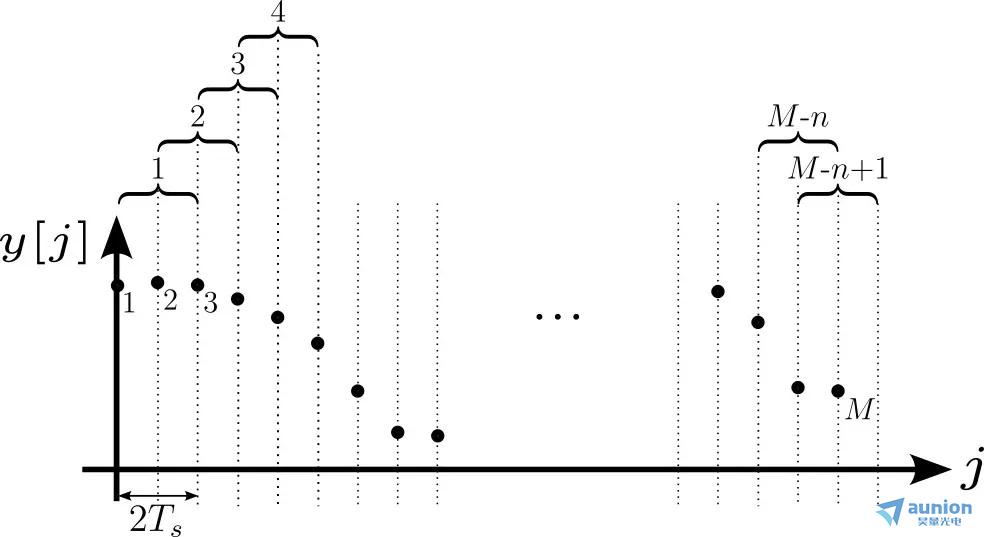
圖 4：為了優(yōu)化使用這些數(shù)據(jù)值，分段會(huì)重疊裙犹。這創(chuàng)建了額外的連續(xù)觀測時(shí)間對(duì)尽狠，所以增加了等式（3）中可能的被加數(shù)數(shù)量。在這個(gè) n = 2 的案例中叶圃，受制于非重疊的分段袄膏，我們可以執(zhí)行減法：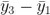
，
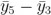等等〔艄冢現(xiàn)在我們還有：
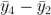沉馆，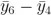
等等。盡管樣本并不完全獨(dú)立，但我們結(jié)果的可信度仍然有所提高斥黑。
在這種情況下
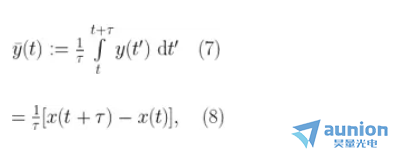
或者用離散函數(shù)表示揖盘，
這樣等式（4）就變成
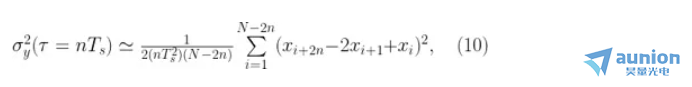
這里 N = M + 1 是 x 的長度。為了理清這一點(diǎn)锌奴，我們可以考慮 y 通過 x 的數(shù)值導(dǎo)數(shù)（差）來構(gòu)造兽狭，因此 M = N ? 1。
這似乎像一個(gè)很抽象的簡化定義缨叫，當(dāng)出于計(jì)算效率的原因椭符，等式（10）提供了 Allan 方差z普遍的方程式。注意這里耻姥，x 測量值提供的是 y 的 Allan 方差，而非 x有咨。
繪制 Allan 方差圖
Allan 方差通常針對(duì)多個(gè)平均時(shí)間進(jìn)行運(yùn)算琐簇，并且以 log - log 刻度繪圖（圖 5）。這樣的圖形有助于確定給定測量值的平均時(shí)間座享。注意我們不會(huì)總是推薦使用較長的平均時(shí)間婉商，特別是存在低頻漂移的情況下。
另外渣叛，常見的噪聲源一般以冪定律描述丈秩，它在 Allan 標(biāo)準(zhǔn)差圖上呈現(xiàn)已知的斜率。例如淳衙，白噪聲會(huì)隨著平均時(shí)間的平方根而減少蘑秽。所以我們能夠預(yù)期白噪聲的斜率為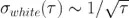 
，情況也確實(shí)如此箫攀。更普遍的是肠牲，如果特定噪聲源在功率譜密度 S 的斜率是 
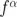，則 Allan 標(biāo)準(zhǔn)差的斜率即 
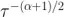靴跛。
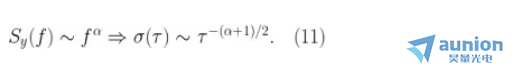
這一事實(shí)使人們能夠輕松確定哪個(gè)噪聲源在不同的平均時(shí)間內(nèi)占主導(dǎo)地位缀雳，建立噪聲預(yù)度以確定系統(tǒng)性能是否得到充分理解，或量化每個(gè)誤差源的分布（圖 6）梢睛。
表 1 羅列了在研究時(shí)鐘和陀螺儀時(shí)常見噪聲源的斜率
表 1：針對(duì)選定應(yīng)用中的不同噪聲源的斜率冪指數(shù)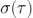 
（即 β 是 
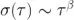）[3, 5]肥印。FM：頻率調(diào)制方式，PM：相位調(diào)制方式绝葡。
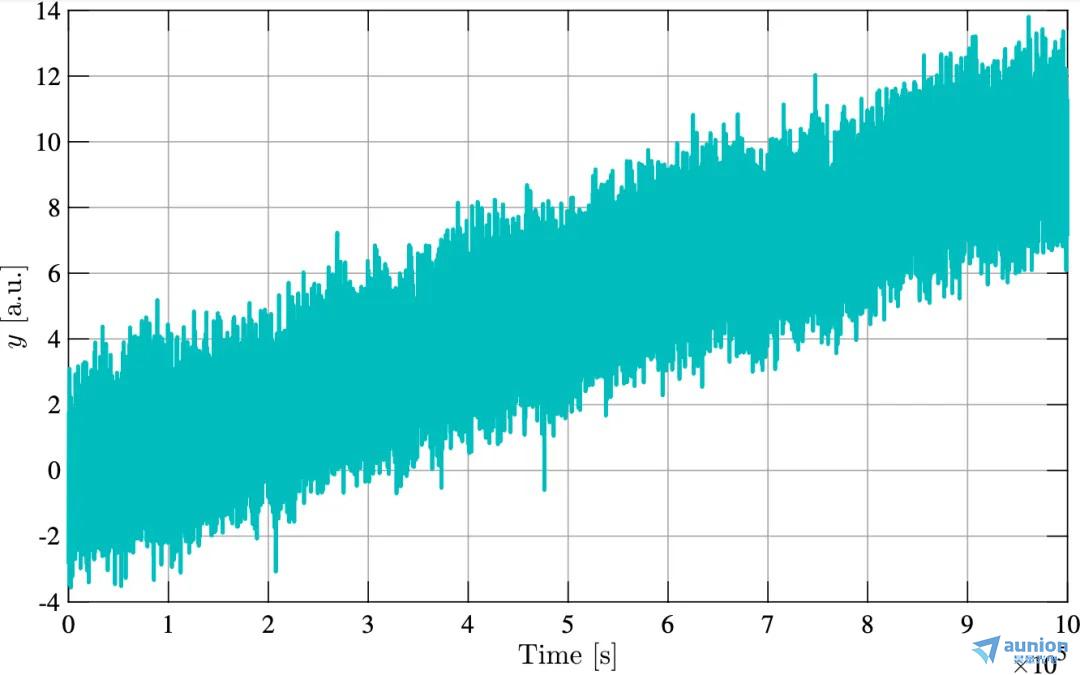
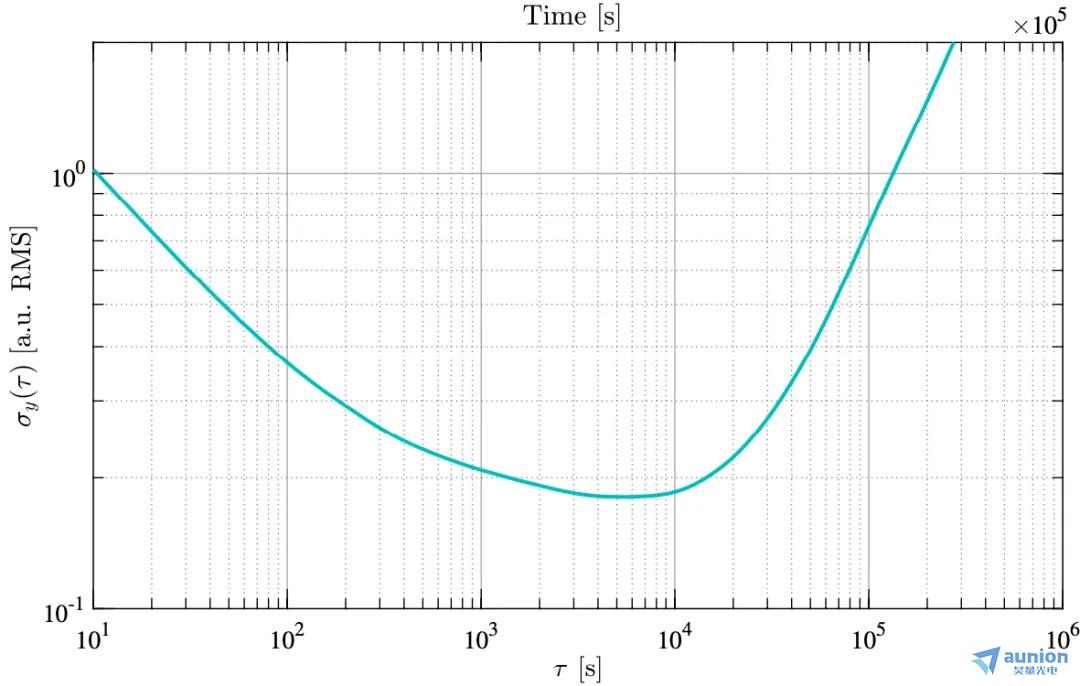
圖 5：時(shí)間序列（上軸）樣例深碱，同時(shí)它相對(duì)應(yīng)的 Allan 標(biāo)準(zhǔn)差圖（下軸）。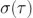
針對(duì)多個(gè)平均時(shí)間 τ 進(jìn)行評(píng)估挤牛，結(jié)果以 log - log 刻度顯示莹痢。
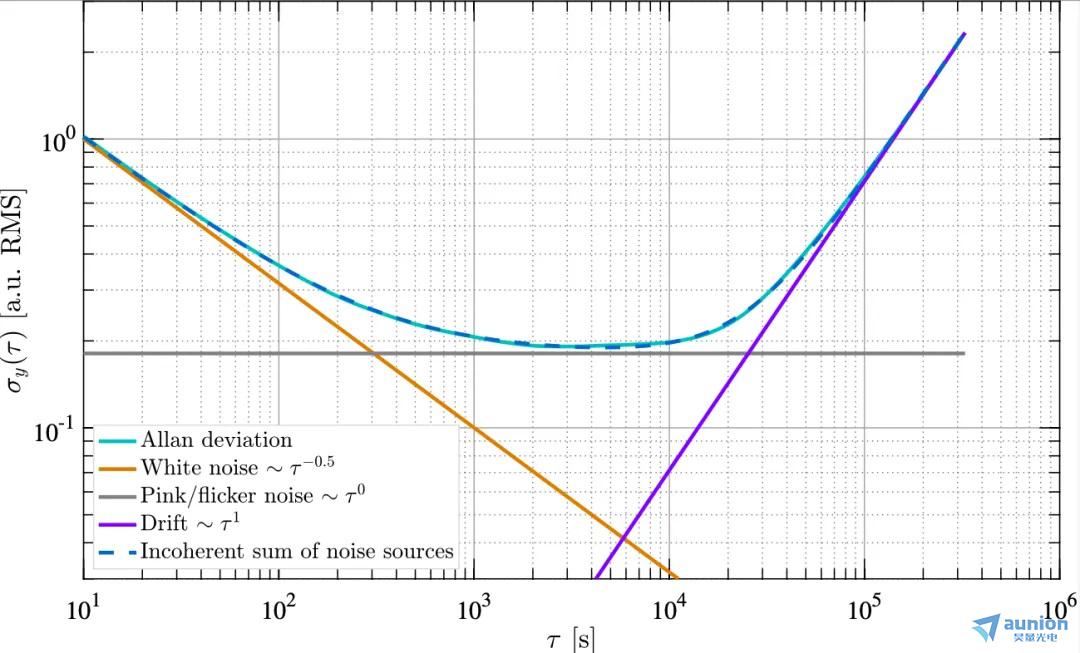
圖 6：冪定律噪聲源在 Allan 標(biāo)準(zhǔn)差圖上顯示為已知的斜率，讓我們可以容易地對(duì)系統(tǒng)噪聲建模【荷牛總的噪聲定義為不相干的獨(dú)立噪聲分布總和航瞭，即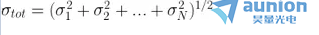 
。在這種情況下坦辟，穩(wěn)定性隨著平均時(shí)間的推移而提高（因?yàn)榘自肼暤挠绊憸p少）刊侯，直到粉紅/閃爍噪聲成為主導(dǎo)。 在較長的時(shí)間尺度上锉走，穩(wěn)定性受到數(shù)據(jù)線性漂移的限制（參見圖 5滨彻，上軸）。 當(dāng)平均時(shí)間約為 5000 秒時(shí)挪蹭，測量結(jié)果很穩(wěn)定亭饵。
如何在Moku配置Allan 方差測量
下方視頻演示如何在Moku配置Allan 方差測量。
視頻鏈接如下：（文章中有視頻）
https://mp.weixin.qq.com/s/8mFEHjThxa84DQOkdpvWnA
功率譜密度 vs Allan 方差
就像我們前面提到的梁厉，有許多的工具可用于描述系統(tǒng)穩(wěn)定性辜羊。雖然 Allan 方差是穩(wěn)定性在時(shí)域上的計(jì)量，那功率譜密度（PSD）词顾，Sy 就是頻域上的對(duì)應(yīng)項(xiàng)八秃。如果 y 的單位是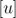 
，則 Sy 的單位是 
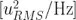肉盹。當(dāng)然在 Allan 方差中所包含的信息 
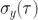只是 PSD 中包含信息的替代表示昔驱，并且存在一個(gè)很接近的轉(zhuǎn)換形式（參考 [6] 中的附錄I）。注意這個(gè)只可以是從 PSD 向 Allan 方差的轉(zhuǎn)換上忍，相反則不行骤肛。轉(zhuǎn)換方程如下：
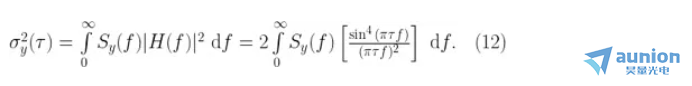
這里 H(f）是時(shí)域采樣函數(shù)的傳遞函數(shù)。
在這個(gè)情況下睡雇，我們需要注意一個(gè)有用的表達(dá)式：
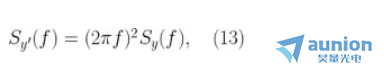
這里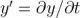 
萌衬。我們可以以此為例，根據(jù) 
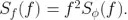轉(zhuǎn)換 相位(φ) 噪聲的 PSD 為頻率 (f) 噪聲之一它抱。
結(jié)果
我們?cè)诒疚闹幸呀?jīng)介紹了 Allan 方差秕豫，展示如何計(jì)算并解釋分析。zui初是在振蕩器穩(wěn)定性的背景下開發(fā)的观蓄，目前仍是很常用的統(tǒng)計(jì)方法混移。不過 ，我們需要強(qiáng)調(diào)它適用于任何時(shí)間序列并且在廣泛的領(lǐng)域中大有用處侮穿。
Allan 方差有助于確定特定測量下的理想觀測時(shí)間并識(shí)別主要的噪聲源歌径。還可以將功率譜密度轉(zhuǎn)換為阿倫方差。
Allan 方差是一種非常有用的統(tǒng)計(jì)工具亲茅，也是 Moku 相位表上可用于數(shù)據(jù)后續(xù)處理的眾多此類工具之一回铛。 其性能以及相位表的微弧度級(jí)精度和 Moku:app 的直觀用戶界面狗准，使 Moku 成為在表征振蕩器系統(tǒng)穩(wěn)定性的應(yīng)用中的設(shè)備。
除 Allan 方差之外
正如標(biāo)準(zhǔn)差存在局限性一樣茵肃，Allan 標(biāo)準(zhǔn)差也不是在所有情況下都是理想的統(tǒng)計(jì)方法腔长。 為了考慮完整，這里簡要討論了 Allan 標(biāo)準(zhǔn)差的兩種常用導(dǎo)數(shù)验残，它們?cè)谀承┣闆r下提供了改善的性能捞附。
修正 Allan 標(biāo)準(zhǔn)差
我們?cè)谏厦孀⒁獾搅嗽?nbsp;Allan 標(biāo)準(zhǔn)差圖上（圖 6）基于梯度軌跡識(shí)別噪聲源的可能性。然而多個(gè)噪聲源會(huì)存在同一個(gè)斜率您没。特別是振蕩器白噪聲相位調(diào)制（WPM）和閃爍噪聲相位調(diào)制（FPM）會(huì)同時(shí)產(chǎn)生一個(gè)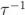 
斜率（如表 1）鸟召。然而，WPM 對(duì)測量帶寬非常靈敏氨鹏，F(xiàn)PM 則不然欧募。通過在 n 個(gè)相鄰測量之間部署額外的平均方法，這里 
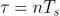喻犁，這樣修正后的 Allan 標(biāo)準(zhǔn)差槽片，產(chǎn)生隨 τ 線性變窄的有效帶寬，同時(shí)能夠區(qū)分這些噪聲源 [7]肢础。
修正的 Allan 標(biāo)準(zhǔn)差可以表示為：
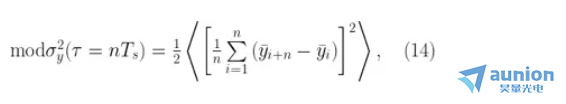
或者更實(shí)際一點(diǎn)，
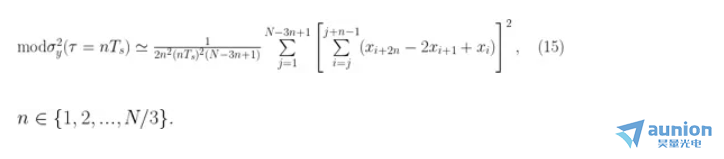
時(shí)間偏差
基于修正的 Allan 標(biāo)準(zhǔn)差更進(jìn)一步的計(jì)量是時(shí)間偏差碌廓，或者時(shí)間 Allan 標(biāo)準(zhǔn)差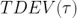 
传轰，可以表示為：
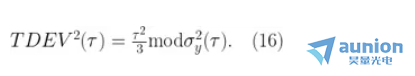
注意這不過是修正 Allan 方差的另一個(gè)版本（所有在 log - log 圖上的斜率通過 τ 的一次冪減少）。選擇歸一化因數(shù)使得當(dāng) n = 1 時(shí)谷婆，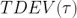
與白相位調(diào)制（PWM）噪聲保持一致慨蛙。
更多詳情請(qǐng)聯(lián)系昊量光電/歡迎直接聯(lián)系昊量光電
關(guān)于昊量光電：
上海昊量光電設(shè)備有限公司是光電產(chǎn)品專業(yè)代理商，產(chǎn)品包括各類激光器纪挎、光電調(diào)制器期贫、光學(xué)測量設(shè)備、光學(xué)元件等异袄，涉及應(yīng)用涵蓋了材料加工通砍、光通訊、生物醫(yī)療烤蜕、科學(xué)研究封孙、國防、量子光學(xué)讽营、生物顯微虎忌、物聯(lián)傳感、激光制造等橱鹏；可為客戶提供完整的設(shè)備安裝膜蠢，培訓(xùn)堪藐，硬件開發(fā)，軟件開發(fā)挑围，系統(tǒng)集成等服務(wù)礁竞。
您可以通過我們昊量光電的官方網(wǎng)站www.wjjzl.com了解更多的產(chǎn)品信息，或直接來電咨詢4006-888-532贪惹。
參考文獻(xiàn)
TDEV 也經(jīng)常用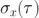 
表示苏章，明確了它是描述 x 穩(wěn)定性（而不是 y）的事實(shí)。這是由于附加因子 τ 造成的奏瞬。
顧名思義枫绅，這種測量在表征時(shí)序分布信號(hào)非常有用，它用于描述時(shí)鐘的相位變化來作為平均時(shí)間的函數(shù)硼端。
[1] D. W. Allan, “Statistics of atomic frequency standards,”IEEE Proceedings, vol. 54, pp. 221–230, Feb. 1966.
[2] L. Hua, Y. Zhuang, L. Qi, J. Yang, and L. Shi, “Noise Analysis and Modeling in visible light Communication Using Allan Variance,”IEEE Access, vol. 6, pp. 74 320–74 327, 2018.
[3] IEEE, “IEEE Standard Specification Format Guide and Test Procedure for Single-Axis Interferometric Fiber Optic Gyros,”IEEE Std 952-1997, pp. 1–84, 1997.
[4] C. A. Greenhall and W. Riley, “Uncertainty of Stability Variances Based on Finite Differences,” September 2004. [Online]. Available:https://ntrs.nasa.gov/citations/20050061319
[5] W. Riley and D. Howe, “NIST Special Publication 1065: Handbook of frequency stability Analysis,” July 2008. [Online]. Available:https://tsapps.nist.gov/publication/getpdf.cfm?pub id=50505
[6] J. A. Barnes, A. R. Chi, L. S. Cutler, D. J. Healey, D. B. Leeson, T. E. McGunigal, J. A. Mullen, W. L. Smith, R. L. Sydnor, R. F. C. Vessot, and G. M. R. Winkler, “Characterization of frequency stability,”IEEE Transactions on Instrumentation and Measurement, vol. IM-20, no. 2, pp. 105–120, 1971.
[7] D. W. Allan and J. A. Barnes, “A Modified “Allan Variance” with In- creased Oscillator Characterization Ability,” inProc. 35th Ann. Freq. Control Symposium. USAERADCOM, Ft. Nonmouth, NJ 07703: Time and Frequency Division, National Bureau of Standards, May 1981, https://tf.nist.gov/general/pdf/560.pdf.
展示全部 
