矩陣術(shù)語和符號
矩陣維度
列向量和行向量
特殊矩陣和向量
筑基：斯坦福 線性動力系統(tǒng)導(dǎo)論——矩陣術(shù)語和符號
1矩陣術(shù)語和符號
●矩陣維度
●列向量和行向量
●特殊矩陣和向量
2矩陣維度
矩陣是放在方括號內(nèi)的矩形數(shù)值數(shù)組
例子：
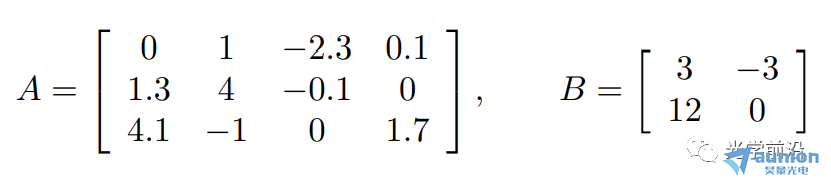
維度(或大小)用行X列表示
●A是一個3X4矩陣，B是一個2X2矩陣
●矩陣A有4列咐旧，B有2行
m=n時驶鹉，m x n矩陣稱為方陣; m
3矩陣系數(shù)
矩陣的元素(或項(entries))是數(shù)組里的值
系數(shù)用兩個下標(biāo)表示行和列來索引
Aij是矩陣A第i行，第j列的值伊约，也稱為A的i,j項
i是Aij的行指數(shù)(index)姚淆，j是Aij的列指數(shù)
(A是矩陣，Aij是值)
例子：
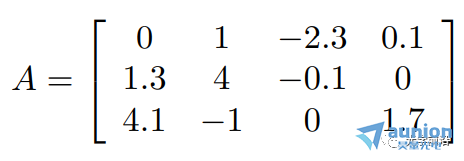
A23=-0.1屡律，A22=4 腌逢，但是A41是無意義的
值為-2.3的項的行指數(shù)是1，它的列指數(shù)是3
4列和行向量
只有一列的矩陣超埋，稱為列向量搏讶，大小為n x 1
只有一行的矩陣，稱為行向量霍殴，大小為1 x n
沒有特別說明的情況下媒惕，“向量”指的是列向量
行和列向量的元素用一個指數(shù)表示，
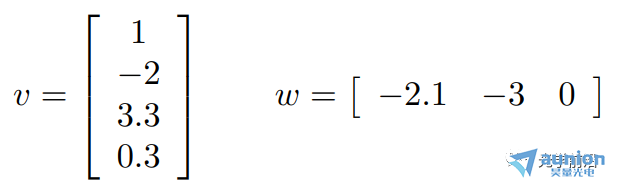
υ是一個列向量(或4 x 1矩陣)来庭，第三項υ3=3.3
ω是一個行向量(或1 x 3矩陣)妒蔚，第三項ω3=0
5矩陣相等
A=B意味著：
●A和B有相同的大小
●相應(yīng)項相等
例子：
●
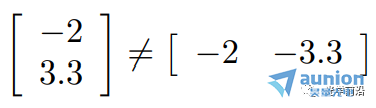，因為維度不一致
●
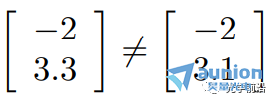月弛，因為第二項不相等
6零矩陣和單位矩陣
0mxn表示大小為m x n的零矩陣肴盏，所有的元素都為0
In表示大小為n x n的單位矩陣，其中
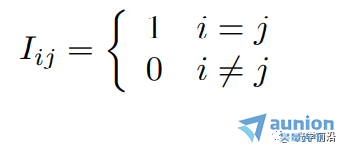
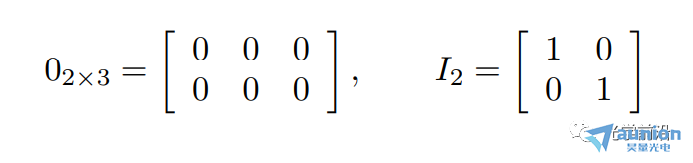
0nx1稱為零向量尊搬；01xn稱為零行向量
約定：下標(biāo)通常不寫叁鉴，所以需要從上下文推測出零矩陣和單位矩陣的大小
7單位向量
ei表示第i個單位向量：它的第i項為1，其它項為0佛寿。如：
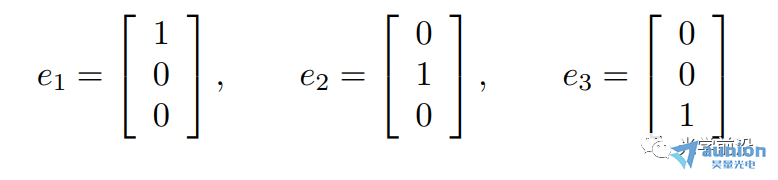
單位向量的大小也需要從語義中推測幌墓。
單位向量是單位矩陣I的列。
有的作者使用1(或e)表示所有元素都是1的向量冀泻，有的時候稱為一向量
維度為2的一向量是：
關(guān)于昊量光電：
上海昊量光電設(shè)備有限公司是國內(nèi)知名光電產(chǎn)品專業(yè)代理商常侣，代理品牌均處于相關(guān)領(lǐng)域的發(fā)展前沿；產(chǎn)品包括各類激光器弹渔、光電調(diào)制器胳施、光學(xué)測量設(shè)備、精密光學(xué)元件等肢专，涉及應(yīng)用領(lǐng)域涵蓋了材料加工舞肆、光通訊焦辅、生物醫(yī)療、科學(xué)研究椿胯、國防及更細(xì)分的前沿市場如量子光學(xué)筷登、生物顯微、物聯(lián)傳感哩盲、精密加工前方、先進(jìn)激光制造等；可為客戶提供完整的設(shè)備安裝廉油，培訓(xùn)惠险，硬件開發(fā)，軟件開發(fā)抒线，系統(tǒng)集成等優(yōu)質(zhì)服務(wù)班巩。
您可以通過昊量光電的官方網(wǎng)站www.wjjzl.com了解更多的產(chǎn)品信息，或直接來電咨詢4006-888-532嘶炭。
本文章經(jīng)光學(xué)前沿授權(quán)轉(zhuǎn)載,商業(yè)轉(zhuǎn)載請聯(lián)系獲得授權(quán)趣竣。
