3D成像機(jī)器視覺基礎(chǔ)知識（二） 視覺系統(tǒng)坐標(biāo)系

正文

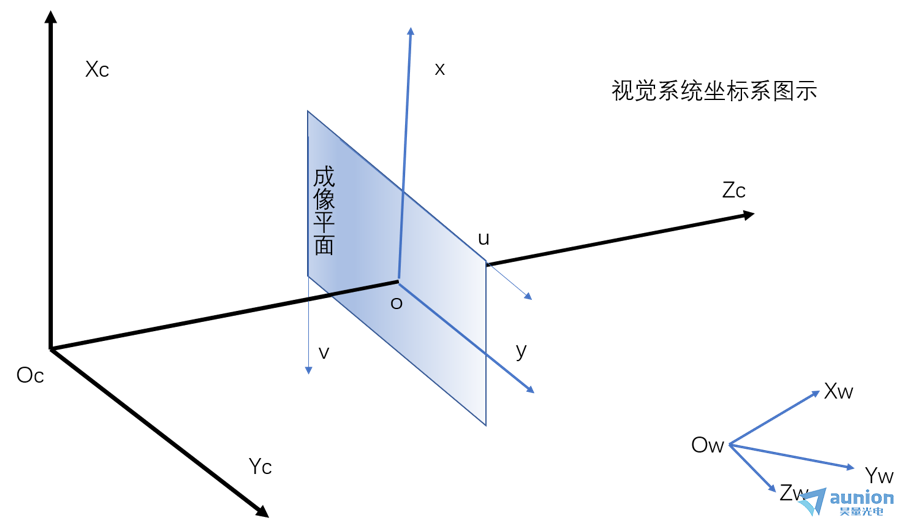
視覺系統(tǒng)中存在三大坐標(biāo)系：世界坐標(biāo)系，攝像機(jī)坐標(biāo)系和圖像坐標(biāo)系立由。三大坐標(biāo)系的關(guān)系見圖示轧钓。其中（Xw,Yw,Zw）為世界坐標(biāo)

系，（Xc,Yc,Zc）為攝像機(jī)坐標(biāo)系锐膜，（u,v）和（x,y）是圖片坐標(biāo)系的兩種表示方法毕箍。

 

世界坐標(biāo)系：是目標(biāo)物體實(shí)際位置的參考系。世界坐標(biāo)可以根據(jù)運(yùn)算方便與否自由定義道盏。在雙目視覺中世界坐標(biāo)系主要用于標(biāo)定時(shí)確定

標(biāo)定物的位置而柑；確定相機(jī)位置以推算出兩個(gè)相機(jī)的相對位置文捶；作為重建得到三維坐標(biāo)的容器，盛放重建后的物體的三維坐標(biāo)媒咳。

攝像機(jī)坐標(biāo)系：攝像機(jī)坐標(biāo)系的原點(diǎn)在攝像機(jī)的光心上粹排，z軸與攝像機(jī)光軸平行，x軸和y軸根據(jù)右手規(guī)則定義涩澡。實(shí)際物體處于世界坐標(biāo)

系中顽耳，通過剛體變換將世界坐標(biāo)系內(nèi)的點(diǎn)和攝像機(jī)坐標(biāo)系內(nèi)的點(diǎn)構(gòu)建一一對應(yīng)的關(guān)系。同時(shí)妙同，攝像機(jī)坐標(biāo)系內(nèi)的點(diǎn)和圖片坐標(biāo)系中的點(diǎn)

也可通過透視投影建立對應(yīng)關(guān)系射富。攝像機(jī)坐標(biāo)系聯(lián)系了圖像坐標(biāo)與世界坐標(biāo)。

圖像坐標(biāo)系:以攝像機(jī)拍攝的二維照片為基準(zhǔn)建立的坐標(biāo)系粥帚。用于指定物體在照片中的位置胰耗。一般傾向?qū)?x,y)稱為連續(xù)圖像坐標(biāo)或空間

圖像坐標(biāo)，將(u,v)稱為離散圖像坐標(biāo)系或者是像素圖像坐標(biāo)系芒涡。這是更能體現(xiàn)其物理意義的叫法柴灯。

(x,y)坐標(biāo)系的原點(diǎn)位于攝像機(jī)光軸與成像平面的交點(diǎn)o上，單位為“米”或者其他長度單位拖陆。(u,v)坐標(biāo)系的原點(diǎn)在圖片的左上角弛槐，單位

為“個(gè)”或者其他數(shù)量單位。 (x,y)主要用于表征物體從攝像機(jī)坐標(biāo)系向圖像坐標(biāo)系的透視投影關(guān)系依啰。而(u,v)則是實(shí)實(shí)在在的，我們能

從攝像機(jī)中得到的真實(shí)信息店枣。

(x,y)與(u,v)存在如下轉(zhuǎn)換關(guān)系：

 

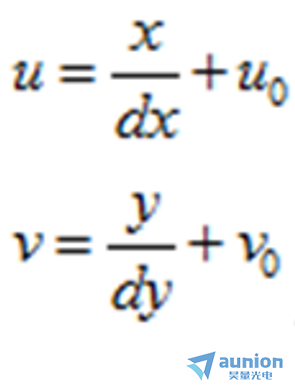
dx代表x軸方向一個(gè)像素的寬度速警，dy代表y軸方向上一個(gè)像素的寬度。dx鸯两、dy為攝像機(jī)的內(nèi)參數(shù)闷旧。(u0,v0)稱為圖像平面的主點(diǎn)，也是攝

像機(jī)的內(nèi)參數(shù)钧唐。其實(shí)相當(dāng)于對x軸和y軸的離散化忙灼。關(guān)于轉(zhuǎn)換和離散將在下文進(jìn)一步說明。

(x,y)與(u,v)的轉(zhuǎn)換關(guān)系運(yùn)用齊次坐標(biāo)可以寫成如下形式：

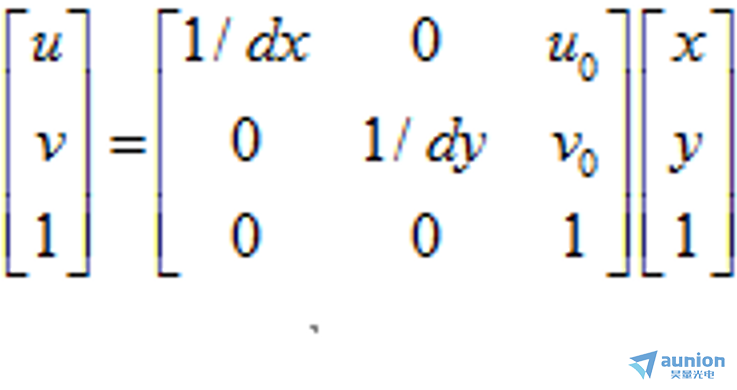
齊次坐標(biāo)的引入方便計(jì)算機(jī)圖形學(xué)進(jìn)行仿射幾何變換钝侠，是機(jī)器視覺中的一個(gè)很好用的數(shù)學(xué)工具该园。上例中的關(guān)系式如果用普通坐標(biāo)則表達(dá)

為：

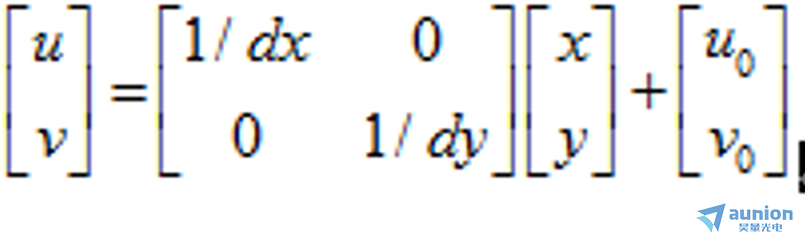
引入齊次坐標(biāo)的形式更利于后續(xù)的計(jì)算。

補(bǔ)充說明：

齊次坐標(biāo)可以簡單理解為將一個(gè)N維向量用N+1維向量進(jìn)行表示帅韧。一個(gè)點(diǎn)(X,Y)在齊次坐標(biāo)里面變成了（x,y,w）里初，并且有X = x/w，Y =

 y/w忽舟。

例如：笛卡爾坐標(biāo)系下（1双妨，2）的齊次坐標(biāo)可以表示為（1淮阐，2，1）刁品，如果點(diǎn)（1泣特，2）移動到無限遠(yuǎn)處，在笛卡爾坐標(biāo)下它變?yōu)?/p>

(∞,∞)挑随，然后它的齊次坐標(biāo)表示為（1状您，2，0）镀裤，因?yàn)?1/0, 2/0) = (∞,∞) 竞阐。

您可以通過我們的官方網(wǎng)站了解更多的產(chǎn)品信息，或直接來電咨詢4006-888-532暑劝。