在一個變形系統(tǒng)中舟铜，只有兩條線性無關的近軸光線，所有其他的近軸光線都可以表示為這兩條已知的近軸光線的線性組合奠衔。
變形系統(tǒng)系列（九）-變形系統(tǒng)的近軸像性質-第二部分
眾所周知归斤，在RSOS中只有兩條獨立的近軸光線痊夭。通常我們取邊緣光線和主光線，任何第三條近軸光線都可以寫成這兩者的線性組合脏里。
類似地她我，在一個變形系統(tǒng)中，由下列兩式
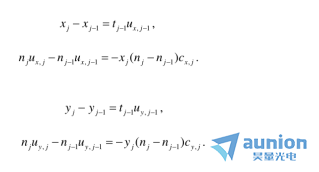
我們也可以證明只有兩條線性無關的近軸光線。
為了證明這一點番舆，假設我們有兩條已知的近軸斜射線酝碳，它們在面j上的分量分別為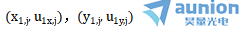
和
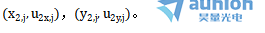這兩條光線線穿過系統(tǒng)的路徑由上兩式完全確定。假設我們還有第三條未知的近軸光線恨狈，我們將其在面j上的相關分量表示為 
假設我們可以把第三個未知近軸光線的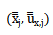 
分量寫成兩個已知近軸光線 
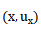分量的組合疏哗，形式如下
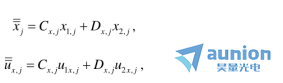
其中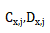
是曲面j上的比例常數(shù)，我們可以通過解這些方程得到它們的值禾怠。
如果我們能證明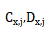
與曲面數(shù)j無關返奉，并且在整個變形系統(tǒng)中都是常數(shù)，那么我們就知道對于這第三條未知的近軸光線吗氏，它的
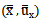分量總是可以表示為兩條已知的近軸光線的線性組合芽偏。如果它的
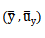分量也成立，我們馬上就能從線性代數(shù)理論中知道第三條光線不能獨立于兩條已知的近軸光線牲证。通過這種方法哮针，我們可以證明在任意變形系統(tǒng)中只有兩條線性無關的近軸光線。
為了證明它坦袍，我們將之前兩個近軸光線追跡方程改寫為如下形式
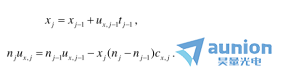
上式適用于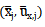
也是因為第三條光線在我們的變形系統(tǒng)中也是近軸光線十厢，因此將上上式帶入上式，我們有
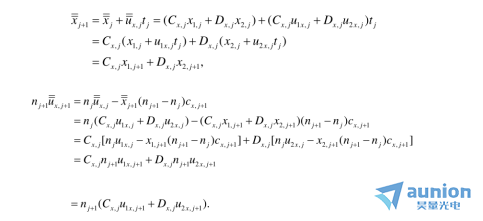
因此我們能夠得到
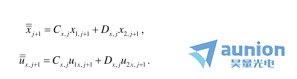
注意捂齐，同樣的過程可以繼續(xù)到下一個表面蛮放，以此類推。
通過比較兩式奠宜，我們看到比例常數(shù)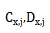
不隨第三條近軸光線通過變形系統(tǒng)而改變包颁。因此，在整個變形系統(tǒng)中压真，它們確實是常數(shù)娩嚼，我們將它們表示為
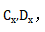因為它們的值不依賴于曲面數(shù)j。
因此滴肿，我們證明了第三條光線的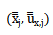
分量岳悟，對于變形系統(tǒng)中的任意面數(shù)j，可以寫成兩個已知的旁軸斜射線的
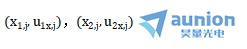分量的線性組合泼差。
同理贵少，可得與y相關的分量：
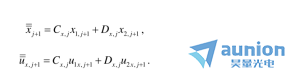
在實際應用中，這兩條已知的近軸光線通常被看作是近軸邊緣光線(來自于軸上物體點堆缘，經過系統(tǒng)光闌邊緣的一點)和近軸主光線(來自于最大物體場上的一點滔灶，經過光闌的中心)。一旦我們知道了這兩條射線吼肥，我們就可以用它們不同的線性組合來形成變形系中所有其他的近軸光線录平。
相關文獻：
《幾何光學 像差 光學設計》（第三版）——李曉彤 岑兆豐
更多詳情請聯(lián)系昊量光電/歡迎直接聯(lián)系昊量光電
關于昊量光電：
上海昊量光電設備有限公司是光電產品專業(yè)代理商麻车，產品包括各類激光器、光電調制器萄涯、光學測量設備绪氛、光學元件等，涉及應用涵蓋了材料加工涝影、光通訊枣察、生物醫(yī)療、科學研究燃逻、國防序目、量子光學、生物顯微伯襟、物聯(lián)傳感猿涨、激光制造等；可為客戶提供完整的設備安裝姆怪，培訓叛赚，硬件開發(fā)，軟件開發(fā)稽揭，系統(tǒng)集成等服務俺附。
您可以通過我們昊量光電的官方網站www.wjjzl.com了解更多的產品信息，或直接來電咨詢4006-888-532溪掀。
展示全部 
展示全部
