

如果一個光學系統的視場較小,其邊緣點可認為與軸上點很靠近,這種近軸物點的像差性質要比遠軸點簡單得多茫多。當光學系統對軸上點成完善像時,使在垂軸方向上與之無限靠近的物點也成完善像的充分必要條件稱為正弦條件 (sine condition)天揖。這就是說,若光學系統滿足正弦條件今膊,就能對小視場物面完善成像些阅。正弦條件可由費馬原理導出。
展示全部 
像差理論與計算系列(四)正弦條件
一缤谎、正弦條件的公式推導
如下圖,光軸上的點 A 成完善像于A’。點B是在過點A 的垂軸方向上無限靠近A 的一點坷澡,設它也被系統成完善像于 B'托呕。分別以y和y'表示AB 和A'B’洋访。過A點的光線OA 與光軸成U 角镣陕,其共軛光線 O'A’與光軸成U’角。
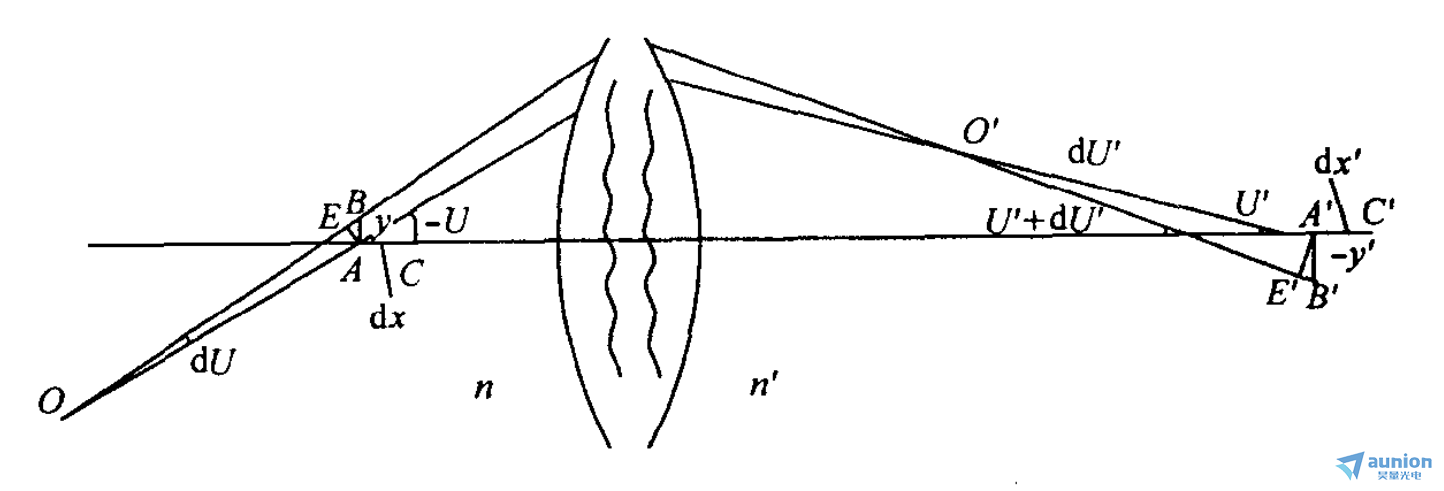
過B點的光線0B 與光軸成 U+dU 角姻政,其共軛光線0'B'與光軸成 U’+ dU’角呆抑。根據費馬原理,光程(OAA’0’)應與(OBB’0’)相等汁展,即
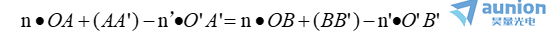
故有
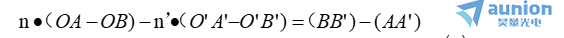 (a)
(a)
以O點為中心,OA為半徑做圓弧食绿,交光線OB于點E侈咕。因dU極小,從?ABE可得
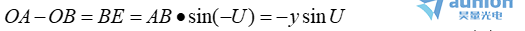 (b)
(b)
同理器紧,在像方可得
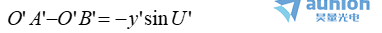 (c)
(c)
將(b)和(c)帶入公式(a),得
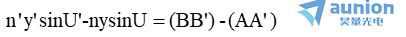
因A’和B’分別是A和B的完善像铲汪,根據費馬原理熊尉,其間的光程各為極值,即
δ(AA’)=δ(BB’)=0,因此光程(AA’)和(BB')各為常數,二者之差也為常數掌腰,該常數可用一條沿光軸的光線來確定狰住。對于這條光線,U=U'=0,故該常數為0,由此得
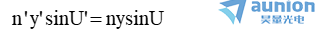
這就是正弦條件齿梁。這是光學系統對垂軸小面積成完善像所需滿足的條件催植。或者說勺择,當軸上點能以寬光束成完善像時创南,若滿足此條件酵幕,過該點的垂軸小面積上的其他店也能以寬光束成完善像扰藕。
所以上述公式由可化為
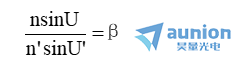
當物體位于無窮遠時芳撒,sinU=0邓深,正弦條件須表示成另一種形式未桥。以-(l-f)/f代替β,并有l(wèi)sinU=h芥备,可導出

顯然,僅由軸上點光線的光路計算結果就能方便地判斷光學系統是否滿足正弦條件。例如邊緣光線萌壳,若已對其校正了球差,并根據其光路計算結果求取比值 nsinU/n' sinU'或h/sinU'袱瓮,它們與按近軸光線所算得的放大率β=nu/nu'或焦距f’=h/u'之差為
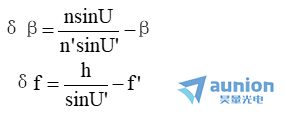
即表示系統偏離正弦條件的程度缤骨。
二、等暈條件
光軸上校正了球差并滿足正弦條件的一對共軛點尺借,稱為齊明點或不暈點绊起。單個折射球面存在三對無球差的共軛點,其中l(wèi)=l’=0和l=l’=r這二對顯然滿足正弦條件,而由l’=(n+n’)r/n’和l=(n+n’)r/n這一對,可得
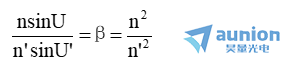
所以,以上三對共軛點都是滿足正弦條件的齊明點燎斩。
正弦條件以軸上點完善成像為前提虱歪。但從球差的討論可知,實際的光學系統僅能對物點發(fā)出的光束中的一個帶或二個帶的光線校正球差,因此,即使是軸上點也不可能是真正的完善成像栅表。此外,軸上點球差校正不佳或不能校正時笋鄙,成像也不完善。此時,軸外近軸點當然也不可能完善成像怪瓶,充其量只能要求它的像質與軸上點一致萧落,即具有相同程度的成像缺陷铐尚,我們稱之為等暈成像 (aplanatic image formation)。
既然軸上點成像時只有球差哆姻,那么,根據等暈成像的要求玫膀,在垂軸平面上與之無限靠近的軸外點也只有球差矛缨,并且對應孔徑角球差相等,二者具有相同的光束結構帖旨,如下圖所示。
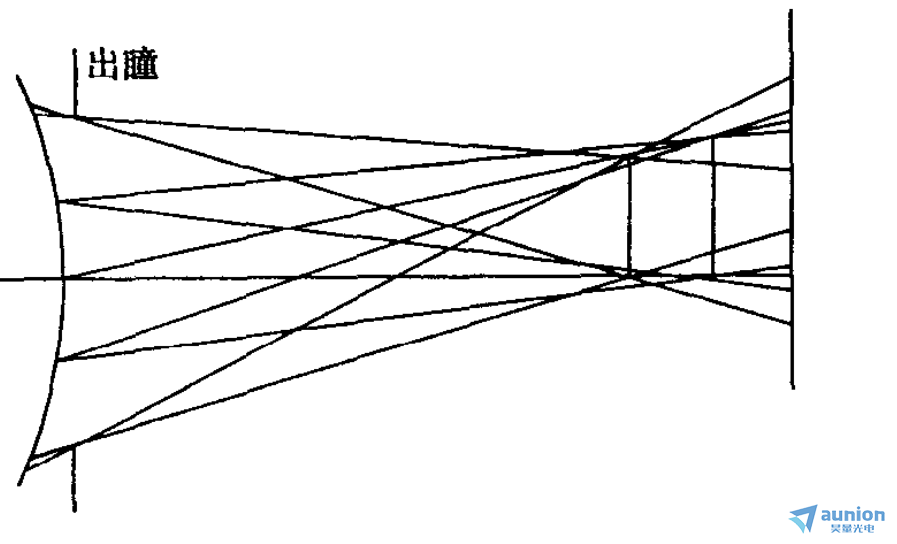
這時所要滿足的條件稱等暈條件(aplanatic condition)解阅。即
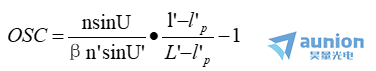
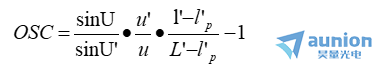
若OSC=0,表示系統滿足等暈條件,OSC 稱為正弦差落竹。當軸上點由于球差而不完善成像時,滿足此條件可使垂軸小面積等暈成像货抄。
從以上公式可見,為計算正弦差以判斷近軸點的像質述召,只需利用軸上點的光線計算結果,外加一條第二近軸光線的計算即可達到目的朱转。為使正弦差的公式表示得更明確、簡潔和便于計算藤为,將l'=L-δL'代入,并且一般總取u=sinU夺刑,忽略高次小量(即取sin U'=u'和L’=l后缅疟,上述公式可化為
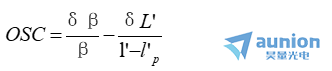
當物體位于無窮遠時,按公式lsinU=h遍愿,可將上式表示成
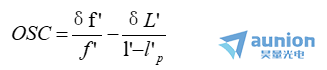
以上二式中,δβ和δf’分別由之前他們對應的表達式決定噪径。
以上計算正弦差的公式中,都包含有出瞳位置因子l’p,它隨孔徑光闌位置而變变屁。因此,當系統的球差已定而不滿足等暈條件時,一定可以找到一個光闌位置使系統的正弦差為零令宿。挑選光闌位置來校正某一種與其有關的像差是光學設計時常用手段寇荧。
相關文獻:《幾何光學 像差 光學設計》(第三版)——李曉彤 岑兆豐
您可以通過我們的官方網站了解更多的產品信息,或直接來電咨詢4006-888-532羞海。
展示全部 